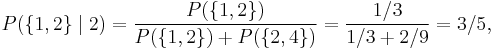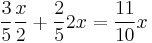Two envelopes problem
The two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle or paradox in logic, philosophy, probability and recreational mathematics, of special interest in decision theory and for the Bayesian interpretation of probability theory. Historically, it arose as a variant of the necktie paradox.
A statement of the problem starts with:
Let us say you are given two indistinguishable envelopes, each of which contains a positive sum of money. One envelope contains twice as much as the other. You may pick one envelope and keep whatever amount it contains. You pick one envelope at random but before you open it you are offered the possibility to take the other envelope instead.
It is possible to give arguments that show that it will be to your advantage to swap envelopes by showing that your expected return on swapping exceeds the sum in your envelope. This leads to the logical absurdity that it is beneficial to continue to swap envelopes indefinitely.
A large number of different solutions have been proposed. The usual scenario is that one writer proposes a solution that solves the problem as stated, but then some other writer discovers that by altering the problem a little the paradox is brought back to life again. In this way a family of closely related formulations of the problem is created which are then discussed in the literature.
It is quite common for authors to claim that the solution to the problem is easy, even elementary.[1] However, when investigating these elementary solutions they are not the same from one author to the next. Currently, at least a couple of new papers are published every year.[2]
Contents |
The problem
The basic setup: You are given two indistinguishable envelopes, each of which contains a positive sum of money. One envelope contains twice as much as the other. You may pick one envelope and keep whatever amount it contains. You pick one envelope at random but before you open it you are offered the possibility to take the other envelope instead.[3]
The switching argument: Now suppose you reason as follows:
- I denote by A the amount in my selected envelope.
- The probability that A is the smaller amount is 1/2, and that it is the larger amount is also 1/2.
- The other envelope may contain either 2A or A/2.
- If A is the smaller amount the other envelope contains 2A.
- If A is the larger amount the other envelope contains A/2.
- Thus the other envelope contains 2A with probability 1/2 and A/2 with probability 1/2.
- So the expected value of the money in the other envelope is
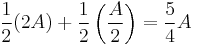
- This is greater than A, so I gain on average by swapping.
- After the switch, I can denote that content by B and reason in exactly the same manner as above.
- I will conclude that the most rational thing to do is to swap back again.
- To be rational, I will thus end up swapping envelopes indefinitely.
- As it seems more rational to open just any envelope than to swap indefinitely, we have a contradiction.
The puzzle: The puzzle is to find the flaw in the very compelling line of reasoning above.
Proposed resolution
This follows from the recognition that the symbol A in step 7 is effectively used to denote two different quantities, committing the fallacy of equivocation. This error is brought into relief if we denote by X the smaller amount, making 2X the larger amount, then reconsider what happens in steps 4 and 5:
4. If A=X then the other envelope contains 2A (or 2X).
5. If A=2X then the other envelope contains A/2 (or X).
Each of these steps treats A as a random variable, assigning a different value to it in each possible case. However, step 7 continues to use A as if it is a fixed variable, still equal in every case. That is, in step 7, 2A is supposed to represent the amount in the envelope if A=2X, while A/2 is supposed to represent the value if A=X. However, we cannot continue using the same symbol A in one equation under these two incompatible assumptions. To do so is equivalent to assuming A=X=2X; which, for nonzero A, implies 1=2.
This resolution was first noted by Bruss and later explored in an exhaustive paper by Nickerson and Falk.[4][5]
Second variant
The solution above doesn't explain what's wrong if the player is allowed to open the first envelope before being offered the option to switch. In this case, A is indeed a fixed variable. Hence, the proposed solution in the first case breaks down and another explanation is needed.
However, the player will not end up switching envelopes indefinitely in this case as the contents of both envelopes are known after the first switch. Instead, the player's twin sibling opens the other envelope without telling the player the amount it contains. Now both will find that it's better to switch due to the same argument. This is contradictory as the player and twin can't both win when switching envelopes with each other.
Proposed resolution
Blachman, Christensen and Utts (1996),[6] and many later authors working in probability theory, pointed out that if the amounts of money in the two envelopes have any proper probability distribution, then it is simply impossible that whatever the amount A=a in the first envelope, it is equally likely that the second contains a/2 or 2a. Thus step 6 of the argument which leads to always switching is a non-sequitur.
In fact in order for step 6 to be true, whatever a might be, the smaller amount of money in the two envelopes must be equally likely to be between 1 and 2, as between 2 and 4, as between 4 and 8 ... and for that matter, as between 1/2 and 1, as between 1/4 and 1/2 ... But there is no way to divide total probability 1 into an infinite number of pieces which are both equal and larger than zero. Yet the smaller amount of money in the two envelopes must have probability larger than zero to be in at least one of the just mentioned ranges!
To see this, suppose that the chance that the smaller of the two envelopes contains an amount between  and
and 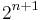 is
is 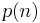 , where n is any whole number, positive or negative, and for definiteness we include the lower limit but exclude the upper in each interval. It follows that the conditional probability that the envelope in our hands contains the smaller amount of money of the two, given that its contents are between
, where n is any whole number, positive or negative, and for definiteness we include the lower limit but exclude the upper in each interval. It follows that the conditional probability that the envelope in our hands contains the smaller amount of money of the two, given that its contents are between 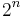 and
and 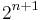 , is
, is 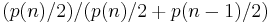 . If this is equal to 1/2, it follows by simple algebra that
. If this is equal to 1/2, it follows by simple algebra that 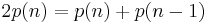 , or
, or 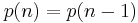 . This has to be true for all n, an impossibility.
. This has to be true for all n, an impossibility.
Third variant
Though probability theory can defuse the second variant of the paradox, it turns out that examples can still easily be found of proper probability distributions, such that the expected value of the amount in the second envelope given that in the first does exceed the amount in the first, whatever it might be.[7]
Denote again the amount of money in the first envelope by A and that in the second by B. We think of these as random. Let X be the smaller of the two amounts and Y=2X be the larger. Notice that once we have fixed a probability distribution for X then the joint probability distribution of A,B is fixed, since A,B = X,Y or Y,X each with probability 1/2, independently of X,Y.
The bad step 6 in the "always switching" argument led us to the finding 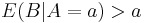 for all a, and hence to the recommendation to switch, whether or not we know a. Now, it turns out that one can quite easily invent proper probability distributions for X, the smaller of the two amounts of money, such that this bad conclusion is still true! (One example is analysed in more detail below). It cannot be true that whatever a, given A=a, B is equally likely to be a/2 or 2a, but it is true that whatever a, given A=a, B is larger in expected value than a.
for all a, and hence to the recommendation to switch, whether or not we know a. Now, it turns out that one can quite easily invent proper probability distributions for X, the smaller of the two amounts of money, such that this bad conclusion is still true! (One example is analysed in more detail below). It cannot be true that whatever a, given A=a, B is equally likely to be a/2 or 2a, but it is true that whatever a, given A=a, B is larger in expected value than a.
Suppose[8] that the envelope with the smaller amount actually contains 2n dollars with probability 2n/3n+1 where n = 0, 1, 2,… These probabilities sum to 1, hence the distribution is a proper prior (for subjectivists) and a completely decent probability law also for frequentists.
A sensible strategy is certainly to swap when the first envelope contains 1, as the other must then contain 2. Now suppose the first envelope contains 2. In this case there are only two possibilities; the envelope pair in front of us is either {1, 2} or {2, 4}, all other pairs are impossible. The conditional probability that it's the {1, 2} pair given the first envelope contains 2 is
and consequently the probability it's the {2, 4} pair is 2/5 since all other envelope pairs have zero conditional probability and the two possibilities must add up to one.
It turns out that these proportions hold in general unless the first envelope contains 1. Thus, denote by x the amount found where x = 2n for some n ≥ 1, then the other envelope contains x/2 with probability 3/5 and 2x with probability 2/5. Note that except for the case that the first envelope contains 1, given the first envelope contains x, the second envelope is more likely to be smaller than larger, yet its conditionally expected amount is larger: the expected gain by switching is
which is more than x. This means that the player should switch in all cases.
But once again, the player may go through this reasoning before opening either envelope, and deduce that the other envelope should always be chosen. This conclusion is just as clearly wrong as it was in the first and second cases. But now the flaws noted above don't apply; the x in the expected value calculation is a known constant (in every single case) and the probabilities in the formula are obtained from a specified and proper prior distribution.
Proposed resolution
Fortunately, the new paradox can be defused again.[9] Suppose 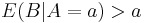 for all a. As remarked before, this is possible for some probability distributions of X (the smaller amount of money in the two envelopes). Averaging over a, it follows either that
for all a. As remarked before, this is possible for some probability distributions of X (the smaller amount of money in the two envelopes). Averaging over a, it follows either that 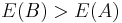 , or alternatively that
, or alternatively that 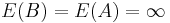 . But A and B have the same probability distribution, and hence the same expectation value, by symmetry (each envelope is equally likely to be the smaller of the two). Thus both have infinite expectation values, and hence so must X too.
. But A and B have the same probability distribution, and hence the same expectation value, by symmetry (each envelope is equally likely to be the smaller of the two). Thus both have infinite expectation values, and hence so must X too.
Thus if we switch for the second envelope because its conditional expected value is larger than what actually is in the first, whatever that might be, we are exchanging an unknown amount of money whose expectation value is infinite for another unknown amount of money with the same distribution and the same infinite expected value. Typically, the chance that the second envelope contains more money than the first decreases as the amount a in the first envelope gets larger and larger.
The average amount of money in both envelopes is infinite. Exchanging one for the other simply exchanges an average of infinity with an average of infinity. The larger the amount of money in the first envelope, the more likely this is the larger amount of the pair, even if the other has a larger expectation value given the specific quantity in the first.
These are the facts of life. And enough resolution of the paradox for those working in probability theory. Probability theory tells us why and when the paradox can occur and explains to us why it gives no cause for worry. In a real-life situation, the expectation of the amount of money in an envelope cannot be infinity, since the total amount of money in the world is bounded; therefore any probability distribution describing the real world would have to assign probability 0 to the amount being larger than the total amount of money on the world, so the expectation of the amount of money under this distribution cannot be infinity. The resolution of the second paradox is that the postulated probability distributions cannot arise in a real-life situation.
Non-probabilistic variant
The logician Raymond Smullyan questioned if the paradox has anything to do with probabilities at all. He did this by expressing the problem in a way which doesn't involve probabilities. The following plainly logical arguments lead to conflicting conclusions:
- Let the amount in the envelope chosen by the player be A. By swapping, the player may gain A or lose A/2. So the potential gain is strictly greater than the potential loss.
- Let the amounts in the envelopes be Y and 2Y. Now by swapping, the player may gain Y or lose Y. So the potential gain is equal to the potential loss.
Proposed resolutions
A number of solutions have been put forward. Albers, Kooi, and Schaafsma (2005) consider that without adding probability (or other) ingredients to the problem, Smullyan's arguments do not give any reason to swap or not to swap, in any case. Thus there is no paradox. This dismissive attitude is common among writers from probability and economics: Smullyan's paradox arises precisely because he takes no account whatever of probability or utility.
Rather careful and often highly technical analyses have been made by many authors from the field of logic. Though solutions differ, they all pinpoint semantic issues concerned with counterfactual reasoning. We want to compare the amount that we would gain by switching if we would gain by switching, with the amount we would lose by switching if we would indeed lose by switching. However, we cannot both gain and lose by switching at the same time. We are asked to compare two incompatible situations. Only one of them can factually occur, the other will be a counterfactual situation, somehow imaginary. In order to compare them at all, we must somehow "align" the two situations, we must give them some definite points in common.
James Chase (2002), for instance, argues that the second argument is correct because it does correspond to the way to align two situations (one in which we gain, the other in which we lose) which is preferably indicated by the problem description.[10] Also Bernard Katz and Doris Olin (2007) argue this point of view.[11]
In the second argument, we consider the amounts of money in the two envelopes as being fixed; what varies is which one is first given to the player. Because that was an arbitrary and physical choice, the counterfactual world in which the player, counterfactually, got the other envelope to the one he was actually (factually) given is a highly meaningful counterfactual world and hence the comparison between gains and losses in the two worlds is meaningful. This comparison is uniquely indicated by the problem description, in which two amounts of money are put in the two envelopes first, and only after that is one chosen arbitrarily and given to the player. In the first argument, however, we consider the amount of money in the envelope first given to the player as fixed and consider the situations where the second envelope contains either half or twice that amount. This would only be a reasonable counterfactual world if in reality the envelopes had been filled as follows: first, some amount of money is placed in the specific envelope which will be given to the player; and secondly, by some arbitrary process, the other envelope is filled (arbitrarily or randomly) either with double or with half of that amount of money.
On the other hand Byeong-Uk Yi (2009) argues that comparing the amount you would gain if you would gain by switching with the amount you would lose if you would lose by switching is a meaningless exercise from the outset.[12] According to his analysis, all three conclusions are false (or meaningless). He analyses Smullyan's arguments in detail, showing that intermediate steps are being taken, and pinpointing exactly where an incorrect inference is made.
Foundations of mathematical economics
In mathematical economics and the theory of utility, which explains economic behaviour in terms of expected utility, there remains a problem to be resolved.[13] In the real world we presumably wouldn't indefinitely exchange one envelope for the other (and probability theory, as just discussed, explains quite well why calculations of conditional expectations might mislead us). Yet the expected utility based theory of economic behaviour says (or assumes) that people do in practice make economic decisions by maximizing expected utility, and hence predicts that people would switch indefinitely.
Fortunately for mathematical economics and the theory of utility, it is generally agreed that as an amount of money increases, its utility to the owner increases less and less, and ultimately there is a finite upper bound to the utility of all possible amounts of money. We can pretend that the amount of money in the whole world is as large as we like, yet the owner of all that money will not have more and more use of it, the more is in his possession. For decision theory and utility theory, the two envelope paradox illustrates that unbounded utility does not exist in the real world, so fortunately there is no need to build a decision theory which allows unbounded utility, let alone utility of infinite expectation.
Controversy among theoretical economists
As mentioned above, any distribution producing this variant of the paradox must have an infinite mean. So before the player opens an envelope the expected gain from switching is "∞ − ∞", which is not defined. In the words of Chalmers this is "just another example of a familiar phenomenon, the strange behaviour of infinity".[14] Chalmers suggests that decision theory generally breaks down when confronted with games having a diverging expectation, and compares it with the situation generated by the classical St. Petersburg paradox.
However, Clark and Shackel argue that this blaming it all on "the strange behaviour of infinity" doesn't resolve the paradox at all; neither in the single case nor the averaged case. They provide a simple example of a pair of random variables both having infinite mean but where one is always better to choose than the other.[15] This is the best thing to do at every instant as well as on average, which shows that decision theory doesn't necessarily break down when confronted with infinite expectations.
Many mathematical economists are happy to exclude infinite expected utility by assumption, hence excluding the paradox altogether. Some try to generalise some of the existing theory to allow infinite expectations. They are stuck with the paradoxical example just given.
Extensions to the Problem
McDonnell and Abbott analyze a modified problem in which the player is allowed to look in the first envelope before deciding whether to switch or to stay.[16]
They also allow the arranger of the game to decide which amount will be given to the player, with the smaller amount given with probability p and the larger amount with probability 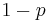 . Thus
. Thus 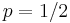 corresponds to the case when the player is given one of the two envelopes completely at random, as in the original problem.
corresponds to the case when the player is given one of the two envelopes completely at random, as in the original problem.
In their analyses, McDonnell and Abbott represent the values in the two envelopes by two random variables. This could either express the subjective beliefs of the player concerning the unknown values in the two envelopes in just one play of the game, or it could express a frequentist model where we imagine the game played many times and the numbers in the envelopes being fixed by a physical randomization procedure. Either way, the lower amount of money X, is thought of as drawn from some probability distribution, and the second amount is then 2X.
In fact, there is no uniform probability distribution over all the real numbers. However, McDonnell and Abbott do work first formally with the situation that X is drawn from a uniform distribution over the interval 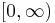 and
and 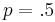 . This can be done, since in the Bayesian calculations, where one wants to condition on the observed value of the amount of money in one of the two envelopes, one only needs to know the prior density of X up to proportionality, so one can formally go through the usual calculations with a uniform prior density, even though there is no uniform prior distribution over the whole real line. This is one popular way to mathematically represent subjectivist total ignorance of the amounts of money in the two envelopes, but in Bayesian statistics it is called an improper prior distribution, and it is well known that use of such non-normalizable prior densities can lead to incorrect deductions. Note that this prior distribution implies that for any number x, the player finds it infinitely more likely that the smaller amount of money is larger than x than that it is smaller than x! (In Bayesian statistics, the prior for a completely unknown positive number is actually conventionally more often taken as the improper prior density 1/x).
. This can be done, since in the Bayesian calculations, where one wants to condition on the observed value of the amount of money in one of the two envelopes, one only needs to know the prior density of X up to proportionality, so one can formally go through the usual calculations with a uniform prior density, even though there is no uniform prior distribution over the whole real line. This is one popular way to mathematically represent subjectivist total ignorance of the amounts of money in the two envelopes, but in Bayesian statistics it is called an improper prior distribution, and it is well known that use of such non-normalizable prior densities can lead to incorrect deductions. Note that this prior distribution implies that for any number x, the player finds it infinitely more likely that the smaller amount of money is larger than x than that it is smaller than x! (In Bayesian statistics, the prior for a completely unknown positive number is actually conventionally more often taken as the improper prior density 1/x).
There is no constant switching strategy that will improve the player's expectations. However, in the case where 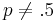 , not surprisingly, the player can improve his expectation by always switching (when
, not surprisingly, the player can improve his expectation by always switching (when 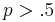 ) or never switching (when
) or never switching (when 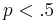 ).
).
A player can take advantage of different probability distributions for X, if he would know this distribution. If probability is taken in the subjectivist sense, then the distribution of X simply represents the player's initial beliefs as to the prior likelihood of different values of x, and so is known, by definition. As a practical matter, the arranger of the game will likely have a limit on the amount of money he can put in the envelopes. As such, he would likely limit the distribution of X to the range ![[0, K]](/2012-wikipedia_en_all_nopic_01_2012/I/16e052f8ee012f00a6fa7245dd3b0f2b.png) , where K is some fixed limit. In this case, it is also possible to increase our expectation by switching when we observe small amounts of money in the envelope and keeping the envelope when it contains a large amount. The threshold between "small" and "large" is subjective and can be fixed at different values, but it should be possible to take advantage of the fact that some of the larger values seen in the game can only be the 2X amount, as these are drawn from a larger domain over
, where K is some fixed limit. In this case, it is also possible to increase our expectation by switching when we observe small amounts of money in the envelope and keeping the envelope when it contains a large amount. The threshold between "small" and "large" is subjective and can be fixed at different values, but it should be possible to take advantage of the fact that some of the larger values seen in the game can only be the 2X amount, as these are drawn from a larger domain over ![[0, 2K]](/2012-wikipedia_en_all_nopic_01_2012/I/a0240f60c1c16b2f42ad03feab7eb963.png) . It should thus be advantageous to keep the larger values when there is a greater likelihood that they come from the range
. It should thus be advantageous to keep the larger values when there is a greater likelihood that they come from the range ![[K, 2K]](/2012-wikipedia_en_all_nopic_01_2012/I/b29d2d49a167dbecaec8fe9de99ad1ba.png) .
.
Thinking of the arranger of the game and the player as two parties in a two person game, puts the problem into the range of game theory. The arranger's strategy consists of a choice of a probability distribution of X. The player's strategy consists of a probability of switching 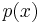 for each possible amount of money he sees in the envelope he opens. Obviously if the player knows the arranger's strategy, the probability distribution of X, then he can compute his optimal switch-or-stay strategy by application of Bayes' theorem. However, what if he doesn't know the arranger's strategy? This connection is further explored in the next section.
for each possible amount of money he sees in the envelope he opens. Obviously if the player knows the arranger's strategy, the probability distribution of X, then he can compute his optimal switch-or-stay strategy by application of Bayes' theorem. However, what if he doesn't know the arranger's strategy? This connection is further explored in the next section.
Randomized solutions
As mentioned before, McDonnell and Abbott consider the situation in which the player is allowed to look in the first envelope before deciding whether to switch or to stay.[16] The player is allowed either to keep this amount, or to switch and take the amount of money in the other envelope, whatever it might be. Is it possible for the player to make his choice in such a way that he goes home with the larger amount of money with probability strictly greater than half?
We are given no information at all about the two amounts of money in the two envelopes, except that they are different, and that neither envelope is empty, in other words, both amounts of money are strictly greater than zero. In particular, we are not told the joint probability distribution of the two numbers. We are not asking for a subjectivist solution. We must think of the two numbers in the envelopes as chosen by the arranger of the game according to some possibly random procedure, completely unknown to us, and fixed. Think of each envelope as simply containing a positive number and such that the two numbers are not the same. The job of the player is to end up with the envelope with the larger number. This variant of the problem, as well as its solution, is attributed by McDonnell and Abbott to information theorist Thomas M. Cover.
Counter-intuitive though it might seem, there is a way that the player can decide whether to switch or to stay so that he has a larger chance than 1/2 of finishing with the bigger sum of money, however the two numbers are chosen by the arranger of the game. However, it is only possible with a so-called randomized algorithm, that means to say, the player needs himself to be able to generate random numbers. Suppose he is able to think up a random amount of money, let's call it Z, such that the probability that Z is larger than any particular quantity z is exp(-z). Note that exp(-z) starts off equal to 1 at z=0 and decreases strictly and continuously as z increases, tending to zero as z tends to infinity. So the chance is 0 that Z is exactly equal to any particular amount of money, and there is a positive probability that Z lies between any two particular different amounts of money. The player compares his Z with the amount of money in the envelope he is given first. If Z is smaller he keeps the envelope. If Z is larger he switches to the other envelope.
Think of the two amounts of money in the envelopes as fixed (though of course unknown to the player). Think of the player's random Z as a probe with which he decides whether the number in the first envelope is small or large. If it is small compared to Z he will switch, if it is large compared to Z he will stay.
If both amounts of money are smaller than the player's Z then his strategy does not help him, he ends up with the second envelope, which is equally likely to be the larger or the smaller of the two. If both amounts of money are larger than Z his strategy does not help him either, he ends up with the first envelope, which again is equally likely to be the larger or the smaller of the two. However if Z happens to be in between the two amounts, then his strategy leads him correctly to keep the first envelope if its contents are larger than those of the second, but to switch to the second if the first envelope has smaller contents than the second. Altogether, this means that he ends up with the envelope with the larger amount of money with probability strictly larger than 1/2. To be precise, the probability that he ends with the "winning envelope" is 1/2 + Prob(Z falls between the two amounts of money)/2.
In practice, the number Z we have described could be determined, to any required degree of accuracy, as follows. Toss a fair coin many times, and convert the sequence of heads and tails into a binary fraction: HTHHTH... becomes the binary representation 0.101101.. of some number y. Then Z = - ln (1-y). Note that we just need to toss the coin long enough that we can see for sure whether Z is smaller or larger than the number in the first envelope. So we only ever need to toss the coin a finite number of times.
The particular probability law (the so-called standard exponential distribution) used to generate the random number Z in this problem is not crucial. Any continuous probability distribution over the positive real numbers which assigns positive probability to any interval of positive length will do the job.
This problem can be considered from the point of view of game theory, where we make the game a two-person zero-sum game with outcomes win or lose, depending on whether the player ends up with the lower or higher amount of money. One player chooses the joint distribution of the amounts of money in both envelopes, and the other player chooses the distribution of Z. The game does not have a "solution" (or saddle point) in the sense of game theory. This is an infinite game and von Neumann's minimax theorem does not apply.[17]
History of the paradox
The envelope paradox dates back at least to 1953, when Belgian mathematician Maurice Kraitchik proposed a puzzle in his book Recreational Mathematics concerning two equally rich men who meet and compare their beautiful neckties, presents from their wives, wondering which tie actually cost more money. It is also mentioned in a 1953 book on elementary mathematics and mathematical puzzles by the mathematician John Edensor Littlewood, who credited it to the physicist Erwin Schroedinger. Martin Gardner popularized Kraitchik's puzzle in his 1982 book Aha! Gotcha, in the form of a wallet game:
- Two people, equally rich, meet to compare the contents of their wallets. Each is ignorant of the contents of the two wallets. The game is as follows: whoever has the least money receives the contents of the wallet of the other (in the case where the amounts are equal, nothing happens). One of the two men can reason: "I have the amount A in my wallet. That's the maximum that I could lose. If I win (probability 0.5), the amount that I'll have in my possession at the end of the game will be more than 2A. Therefore the game is favourable to me." The other man can reason in exactly the same way. In fact, by symmetry, the game is fair. Where is the mistake in the reasoning of each man?
In 1988 and 1989, Barry Nalebuff presented two different two-envelope problems, each with one envelope containing twice what's in the other, and each with computation of the expectation value 5A/4. The first paper just presents the two problems, the second paper discusses many solutions to both of them. The second of his two problems is the one which is nowadays the most common and which is presented in this article. Martin Gardner independently mentioned this same version in his 1989 book Penrose Tiles to Trapdoor Ciphers and the Return of Dr Matrix. Since then, the paradox has been most commonly presented in the symmetric two-envelopes form: the two envelopes are filled first, then one is chosen at random, and called Envelope A. Barry Nalebuff's asymmetric variant, often known as the Ali Baba problem, has one envelope filled first, called Envelope A, and given to Ali. Then a coin is tossed to decide whether Envelope B should contain half or twice that amount, and then given to Baba.
See also
- Bayesian probability
- Bertrand's paradox
- Deal or No Deal
- Decision theory
- Double or nothing
- Monty Hall problem
- Necktie paradox
- Newcomb's paradox
- St. Petersburg paradox
- Talk:Two_envelopes_problem/Literature
- Talk:Two_envelopes_problem/Arguments
Notes and references
- ^ McDonnell, Mark D.; Grant, Alex J.; Land, Ingmar; Vellambi, Badri N.; Abbott, Derek; Lever, Ken (2011). "Gain from the two-envelope problem via information asymmetry: on the suboptimality of randomized switching". Proceedings of the Royal Society, A to appear. doi:10.1098/rspa.2010.0541.
- ^ A complete list of published and unpublished sources in chronological order can be found here
- ^ Falk, Ruma (2008). "The Unrelenting Exchange Paradox". Teaching Statistics 30 (3): 86–88. doi:10.1111/j.1467-9639.2008.00318.x.
- ^ Bruss, F.T. (1996). "The Fallacy of the Two Envelopes Problem". The Mathematical Scientist 21 (2): 112–119..
- ^ Falk, Ruma (2006). "The exchange paradox: Probabilistic and cognitive analysis of a psychological conundrum". Thinking & Reasoning 12 (2): 181–213.. and Falk, Ruma (2009). "An inside look at the two envelope paradox". Teaching Statistics 31 (2): 39–41..
- ^ Blachman, N. M.; Christensen, R.; Utts, J. (1996). The American Statistician 50 (1): 98–99.
- ^ Christensen, R.; Utts, J. (1992). The American Statistician 46 (4): 274–276. See also letters to editor and responses by Christensen and Utts by D.A. Binder (1993; vol. 47, nr. 2, p. 160) and Ross (1994; vol. 48, nr. 3, p. 267), and letter with correction to original article by N.M. Blachman, R. Christensen and J.M. Utts (1996; vol. 50, nr. 1, pp. 98-99)
- ^ Here we present some details of a famous example due to John Broome of a proper probability distribution of the amounts of money in the two envelopes, for which
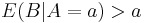 for all a. Broome, John (1995). "The Two-envelope Paradox". Analysis 55 (1): 6–11. doi:10.1093/analys/55.1.6.
for all a. Broome, John (1995). "The Two-envelope Paradox". Analysis 55 (1): 6–11. doi:10.1093/analys/55.1.6. - ^ Binder, D. A. (1993). The American Statistician 47 (2): 160. (letters to the editor, comment on Christensen and Utts (1992)
- ^ Chase, James (2002). "The Non-Probabilistic Two Envelope Paradox". Analysis 62 (2): 157–160. doi:10.1093/analys/62.2.157.
- ^ Katz, Bernard; Olin, Doris (2007). "A tale of two envelopes". Mind 116 (464): 903–926. doi:10.1093/mind/fzm903.
- ^ Byeong-Uk Yi (2009). The Two-envelope Paradox With No Probability. http://philosophy.utoronto.ca/people/linked-documents-people/c%20two%20envelope%20with%20no%20probability.pdf.
- ^ Fallis, D. (2009). "Taking the Two Envelope Paradox to the Limit". Southwest Philosophy Review 25 (2).
- ^ Chalmers, David J. (2002). "The St. Petersburg Two-Envelope Paradox". Analysis 62 (2): 155–157. doi:10.1093/analys/62.2.155.
- ^ Clark, M.; Shackel, N. (2000). "The Two-Envelope Paradox". Mind 109 (435): 415–442. doi:10.1093/mind/109.435.415.
- ^ a b McDonnell, M. D.; Abott, D. (2009). "Randomized switching in the two-envelope problem". Proceedings of the Royal Society A 465 (2111): 3309–3322. doi:10.1098/rspa.2009.0312.
- ^ http://www.mit.edu/~emin/writings/envelopes.html